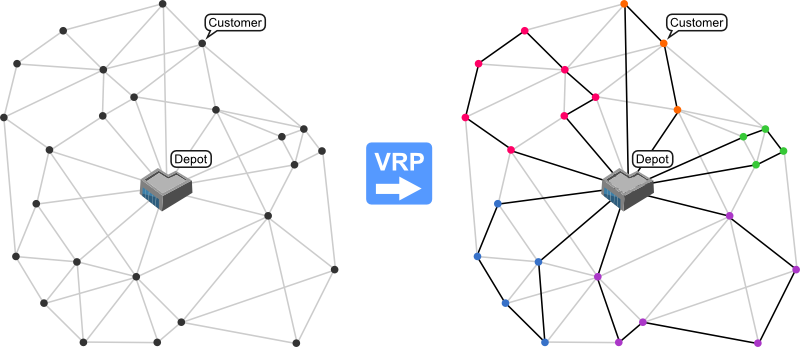
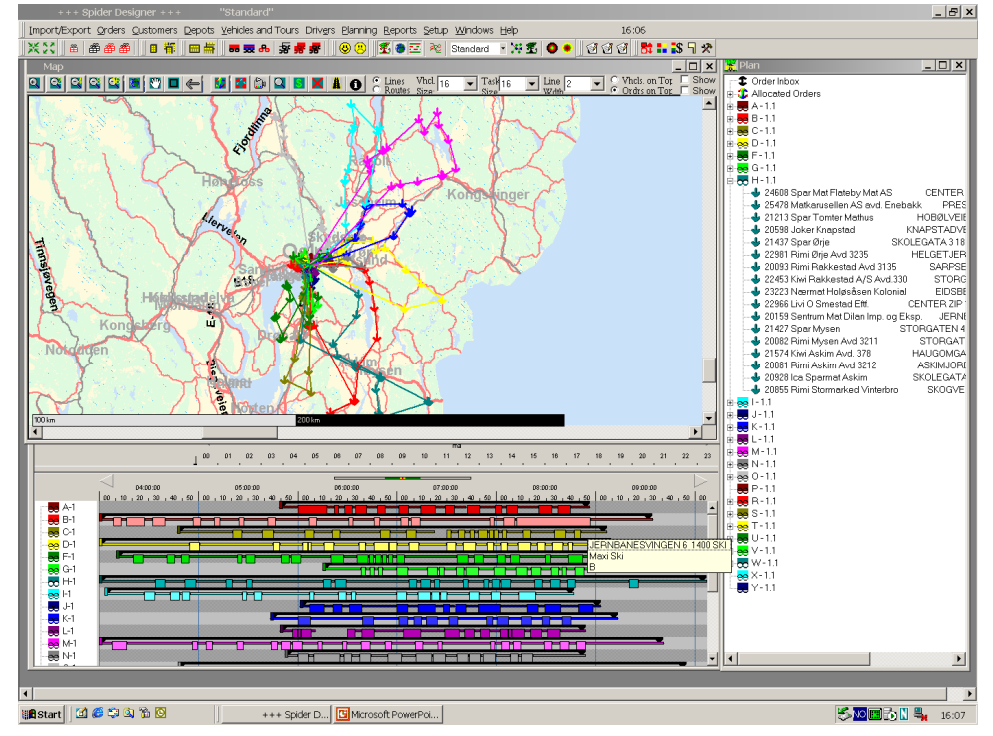
Considerações iniciais
Como o VRP é um problema do mundo real, podemos representar os elementos que compões o VRP de forma matemática G = (V, E) [1].
Seja G = (V, E) um grafo não direcionado, onde V = {v0, v1,…, vn} é o conjunto dos vértices e E = {(vi, vj): vi ,vj ∈ V, i < j} é o conjunto de arestas. O vértice v0 representa o depósito, sendo este a base de uma frota de veículos idênticos de capacidade Q, enquanto os vértices remanescentes correspondem às cidades ou consumidores. Cada consumidor vi tem uma demanda não negativa qi e q0 = 0. Com relação ao número de veículos no depósito, este pode ser limitado ou ilimitado [2].
Outra característica que podemos adicionar ao problema do VRP é uma variável k que adiciona outros vértices aos vértices já existentes de acordo com sua localização, passando a ter a representação de um problema kVRP.
Por que é necessário a variável k?
Imagine que temos o seguinte cenário:
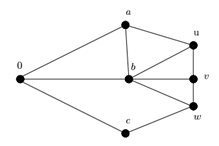
Figura 1: Cenário representado com um Grafo G
O vértice 0 em nosso modelo matemático é o V0, sendo assim, o nosso depósito e ponto de partida inicial e final.
Os vértices a, b, c, u, v e w são respectivamente V = { v1, v2, v3, v4, v5 e v6 } .
Para melhorar a capacidade de entregas, vamos assumir que cada Vn seja um bairro de uma cidade. Próximo a cada bairro, temos casas que receberão a visita do nosso veículo, assim temos o controle de bairros que deverão ser visitados e o que visitar em cada bairro. Logo temos uma nova representação:
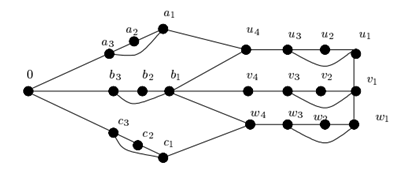
Figura 2: Grafo G’ com adição de K
Na Figura 2, assumimos que k possui valor 3 para os vértices {a, b, c} e k = 4 para os vértices {u, v e w}, tendo assim:
G = O Grafo não direcionado que representa o caminho a ser percorrido.
V = Conjunto de vértices, ou seja, cada casa que ele precisa visitar no grafo G.
E = Conjunto de arestas ( distância entre as casa que serão visitadas) a cada aresta (vi, vj) está associada uma distância não negativa cij que representa a distância entre as casas e ou bairros.
K = Valor de vértices próximos aos vértices iniciais.
Todo esse cenário proposto tem o objetivo de encontrar o menor caminho possível entre os vértices, passando por eles apenas uma vez, e começando e finalizando no ponto inicial V0.
O kVRP é de grande importância quando pensamos em uma transportadora que deseja realizar diversas entregas em uma cidade e quer saber o melhor caminho possível, pois essa otimização, além de reduzir o tempo das entregas, poderá reduzir custos como combustível, desgaste do carro, tempo e etc. [3].
Agora que temos a representação matemática dos elementos que compõem o VRP no mundo real, podemos formular uma hipótese.
Hipótese 1: É possível provar que o problema de roteamento de veículos (VRP) pode ser resolvido em tempo polinomial?
Para essa prova, vamos analisar novamente a Figura 2. Nota-se que os vértices a, b e c tem k = 3 e os vértices w, u e v tem valor k = 4. Por que isso ocorre?
No mundo real não podemos assumir que k sempre terá o mesmo valor. Cada rota de entrega muda constantemente e, portanto, criamos subconjuntos toda vez que o k passa a ter um novo valor.
Analisando a Figura 2, pode-se considerar essa aplicação do mundo real como:
S = conjuntos de novos vértices onde k = 3
T = conjunto de novos vértices onde k = 4.
Sendo assim, na Figura 2, o grafo G’ possui:
S = {a1, a2, a3, b1, b2, b3, c1, c2, c3}
T = {u1, u2, u3, u4, v1, v2, v3, v4, w1, w2, w3, w4}
Prova 1 - Provando que kVRP é resolvido em tempo polinomial
O problema tem solução quando existe um subconjunto E ⊂ S x T de tal forma que o grau de t ∈ T é 2 e o grau de todos s ∈ S é 0 ou 1. Essa característica está relacionada com o bipartite matching problem, problema que é provado ser resolvido em tempo polinomial [4].
Definição da prova 1: O grafo G’ da Figura 2 é construído a partir do grafo G = (V, E) com subconjuntos de vértice {S, T} ⊂ V tal que {S ∪ T} = V \ {0}, assim sendo:
Cada vértice s ∈ S passa a ter três vértices, s1, s2 e s3:
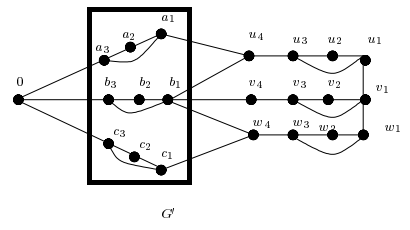
Figura 3: Grafo G’ com destaque em s ∈ S e k = 3.
Na Figura 3, podemos observar o uso de k = 3 assumindo que:
V = {
S = {s1 = {a1, b1, c1}}
S = {s2 = {a2, b2, c3}}
S = {s3 = {c1, b2, c3}}
}
s ∈ S = (0, s3), (s2, s3), (s1, s2) e (s1, s3) onde cada s representa os subconjunto de V.
Com k = 4 cada aresta será (0, s) de tal modo que s ∈ S passa a ter 4 arestas (0, s3), (s2, s3), (s1, s2) e (s1, s3).
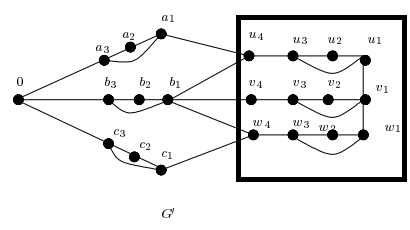
Figura 4: Grafo G’ com destaque em s ∈ S e k = 4.
Na Figura 4, podemos observar o uso de k = 4 assumindo que:
V = {
S = {s1 = {u1, v1, w1}}
S = {s2 = {u2, v2, w2}}
S = {s3 = {u3, v3, w3}}
S = {s4 = {u4, v4, w4}}
}
Cada t ∈ T é substituído por 4 vértices, t1, …, t4, e quatro arestas, (t1, t2), (t2, t3), (t3, t4), e (t1, t3). Uma aresta (s, t) tal que s ∈ t e t ∈ T é substituída por uma borda (s1, t4) e aresta (t, u) de tal modo que t, u ∈ T é substituída por (t1, u1). Nota-se que as arestas de E com duas extremidades em S não estão representadas em G’, como foi visto na Figura 2 em que S = {a, b, c} e T = {u, v, w} [5].
Agora que provamos que a adição de k no problema do VRP caracteriza um grafo bipartidário que é resolvido de forma polinomial, podemos comparar os dois grafos:
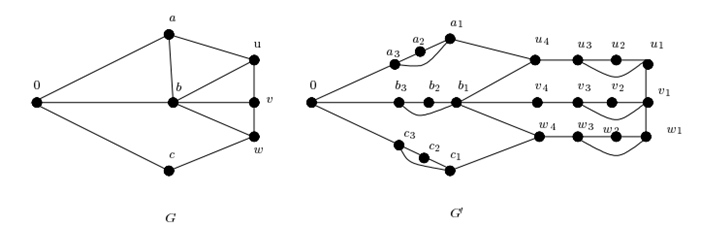
Figura 5: Grafo G e Grafo G’.
Com k = 3 e k = 4 aumentamos a área de cobertura, respeitamos a regra de visitar apenas uma vez cada local e voltar ao ponto de origem 0.
Hipótese 2: Agora que provamos que kVRP pode ser resolvido em tempo polinomial, podemos testar se kVRP é do tipo NP-Completo.
Prova 2 – Provando que kVRP é NP-completo quando k > 3
Para essa prova foi utilizado à técnica de redução por 3-Dimensional Matching, problema provado ser do tipo NP-completo [4]. Primeiramente construímos uma instância 3VRP da seguinte forma:
V = {0} ∪ Vx ∪ Vy ∪ Vm ∪ (∪w ∈ w (Sw ∈ S’w)), onde os vértices Vx, Vy e VM correspondem aos elementos X, Y e M, respectivamente.
E = Ex ∪ Ey ∪ Em ∪ Ex,m ∪ Em,y ∪ (∪w ∈ w Ew), onde:
Ex = {(0,x): x ∈ Vx};
Ey = {(y,0): y ∈ Vy};
Em = {(0,m): m ∈ Vm};
Para cada m = (w, x, y) ∈ M existe um arco (x,m) ∈ Ex,m e um arco (m,y) ∈ Em,y.
Para cada w ∈ W, onde nw é o número de vezes que W está presente em M.
Sw contém nw – 1 vértices, S’w é uma cópia de Sw, e para cada s ∈ Sw é cópia s’ ∈ S’w, Ew contém arcos (s, s’) e (s’, 0), em adição a esses arcos, para cada s ∈ Sw e para cada vértice m ∈ Vm existe uma coordenada w ∈ W, Ew possui um arco (v,s), podemos representar M da seguinte forma:
M = {(x1, w1, y1), (x1, w2, y1), (x1, w2, y2),(x2, w1, y2), (x2, w2, y2)}
A solução de 3VRP existe se e somente se houver um 3-Dimensional Matching M’. Deverá haver uma rota (0, x, w, y, 0) para cada elemento de M’, e todas as outras vértices nw – 1 onde v ∈ Vm correspondem a w devem utilizar (0, v, s, s’, 0) com vértices distintos em s ∈ Sw [6].
Referências:
[1] Lenstra, Jan Karel, and A. H. G. Rinnooy Kan. "Complexity of vehicle routing and scheduling problems." (1981)
[2] Bazgan, Cristina, Refael Hassin, and Jérôme Monnot. "Differential approximation for some routing problems." (2003)
[3] Bräysy, O., et al. A survey of rich vehicle routing models and heuristic solution techniques. Technical report, SINTEF, (2002).
[4] Garey, Michael R., and David S. Johnson. "Computers and intractability : a guide to the theory of NP-completeness." San Francisco: W.H. Freeman (1979).
[5] Haimovich, M. A. R. K., and A. H. G. Rinnooy Kan. "Bounds and heuristics for capacitated routing problems." Mathematics of operations Research 10.4
(1985).
[6] Haimovich, M., Rinnoooy Kan, and Leendert Stougie. "Analysis of heuristics for vehicle routing problems". Universiteit Amsterdam - Institute of Actuarial Sciences and Econometrics. (1988).